Have you ever wondered what is the physical meaning behind the difference of Squares formula which is a² – b² = (a – b)(a + b).

As you can see in the figure 2.1 that a² is divided into 4 parts which are (a – b)², b(a-b), b² and b(a-b).

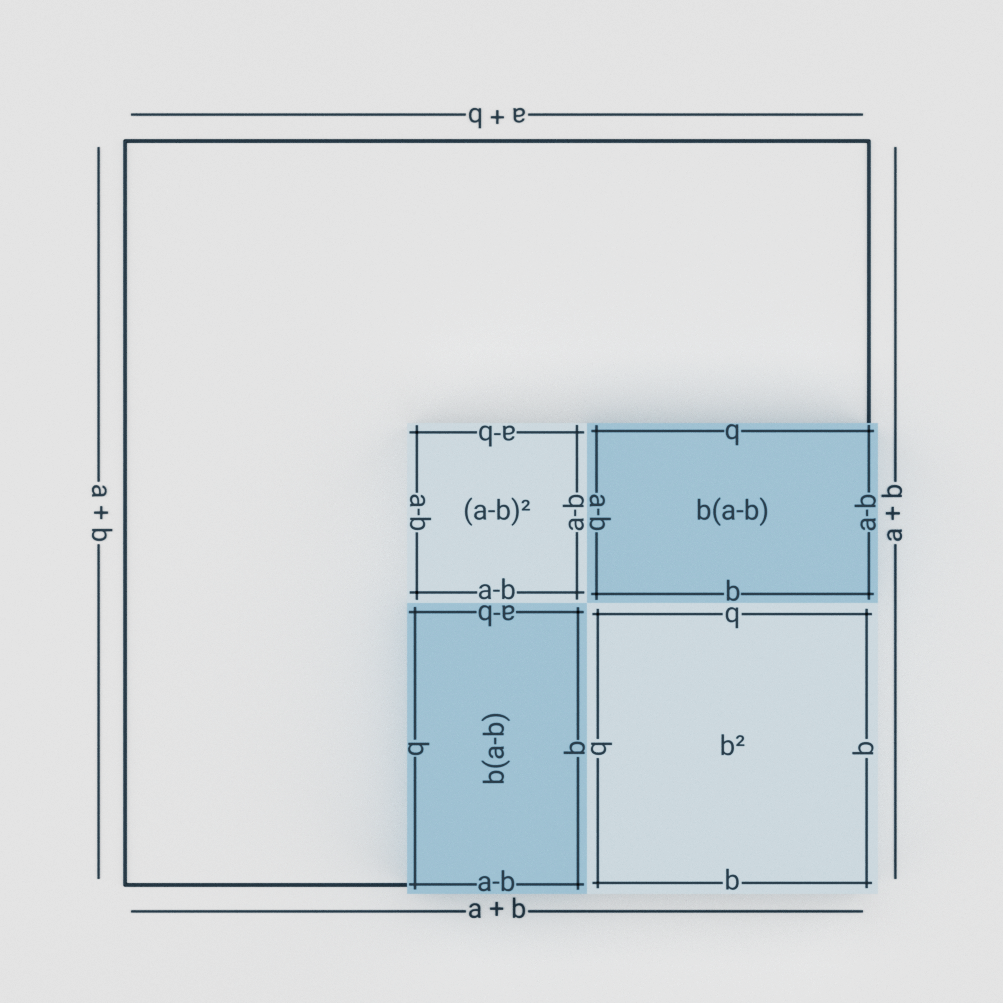
Which basically means that a² = (a – b)² + b² + 2b(a-b) similar to (a + b)² proof.

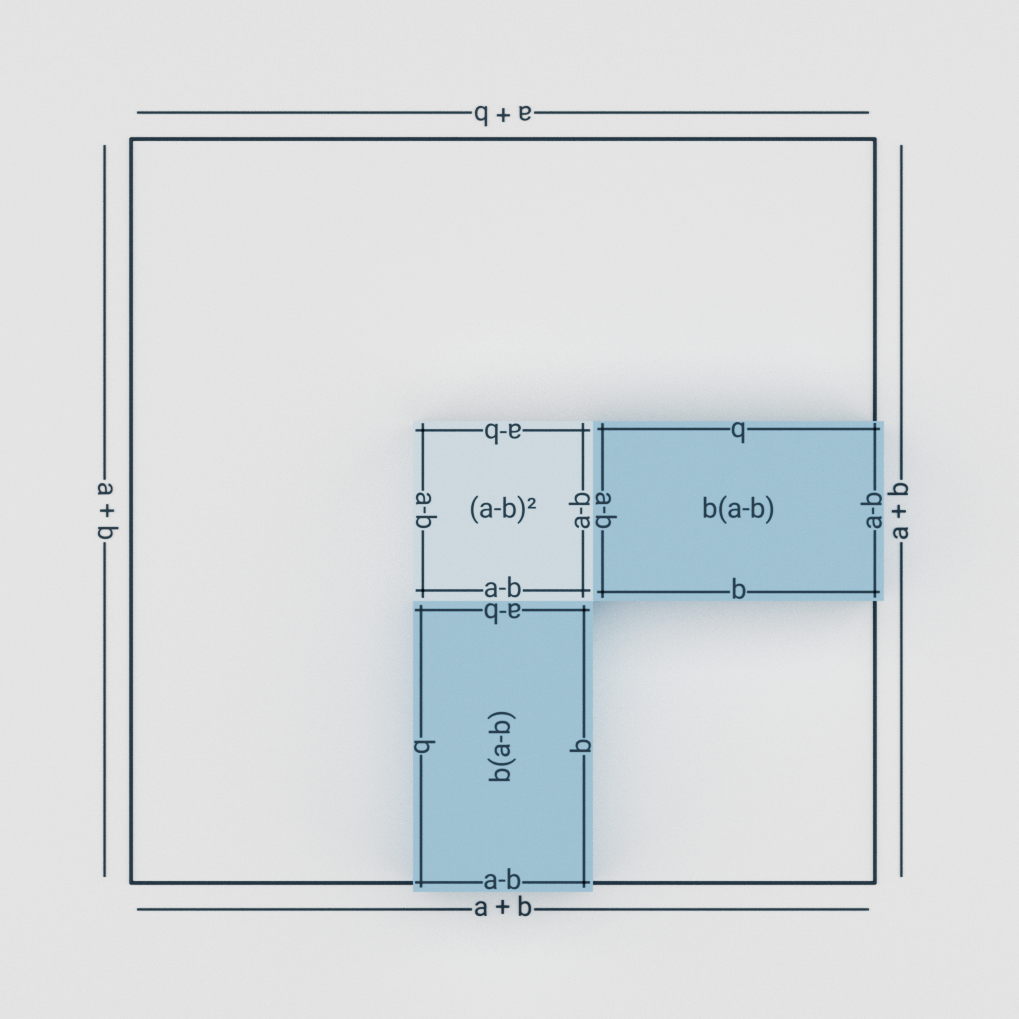
If we remove b² from it, we are left with (a – b)² and 2b(a-b) as shown in figure 2.2, then we are left with a² – b².

Which is the area of this shape (Area = a² – b² ).

Now, rearranged the pieces as shown in figure 2.3

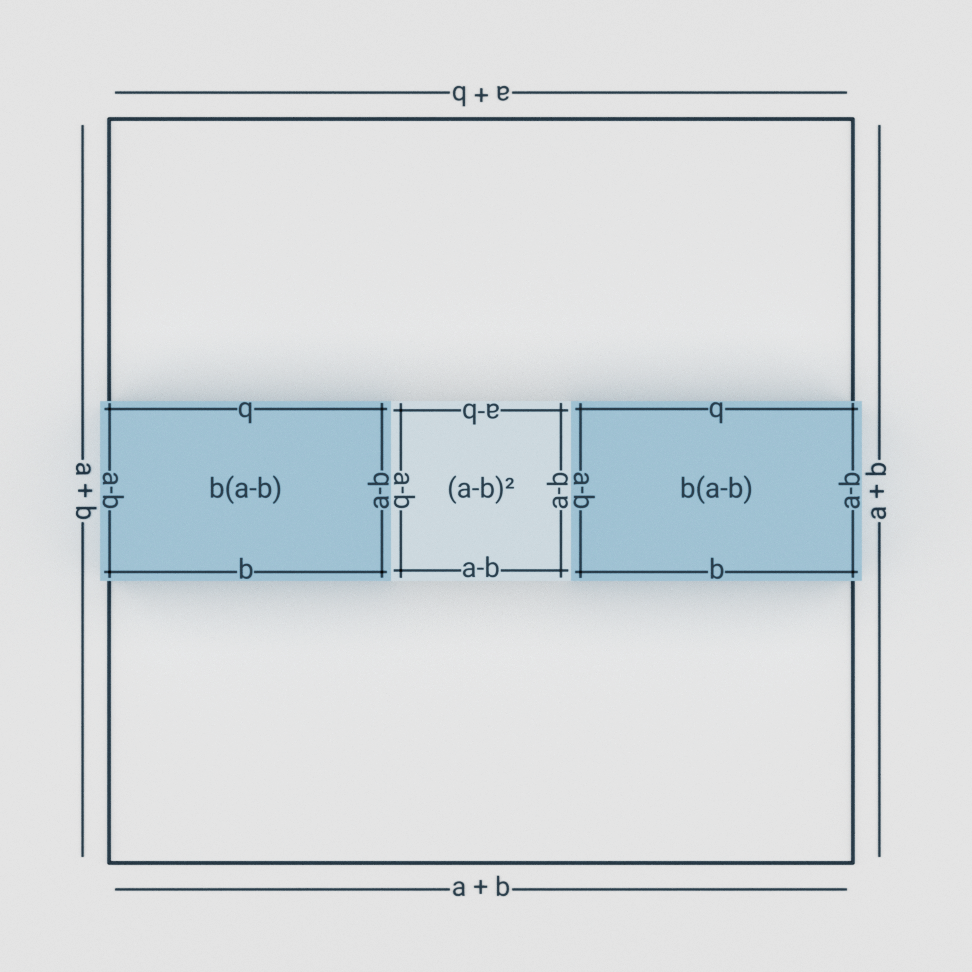
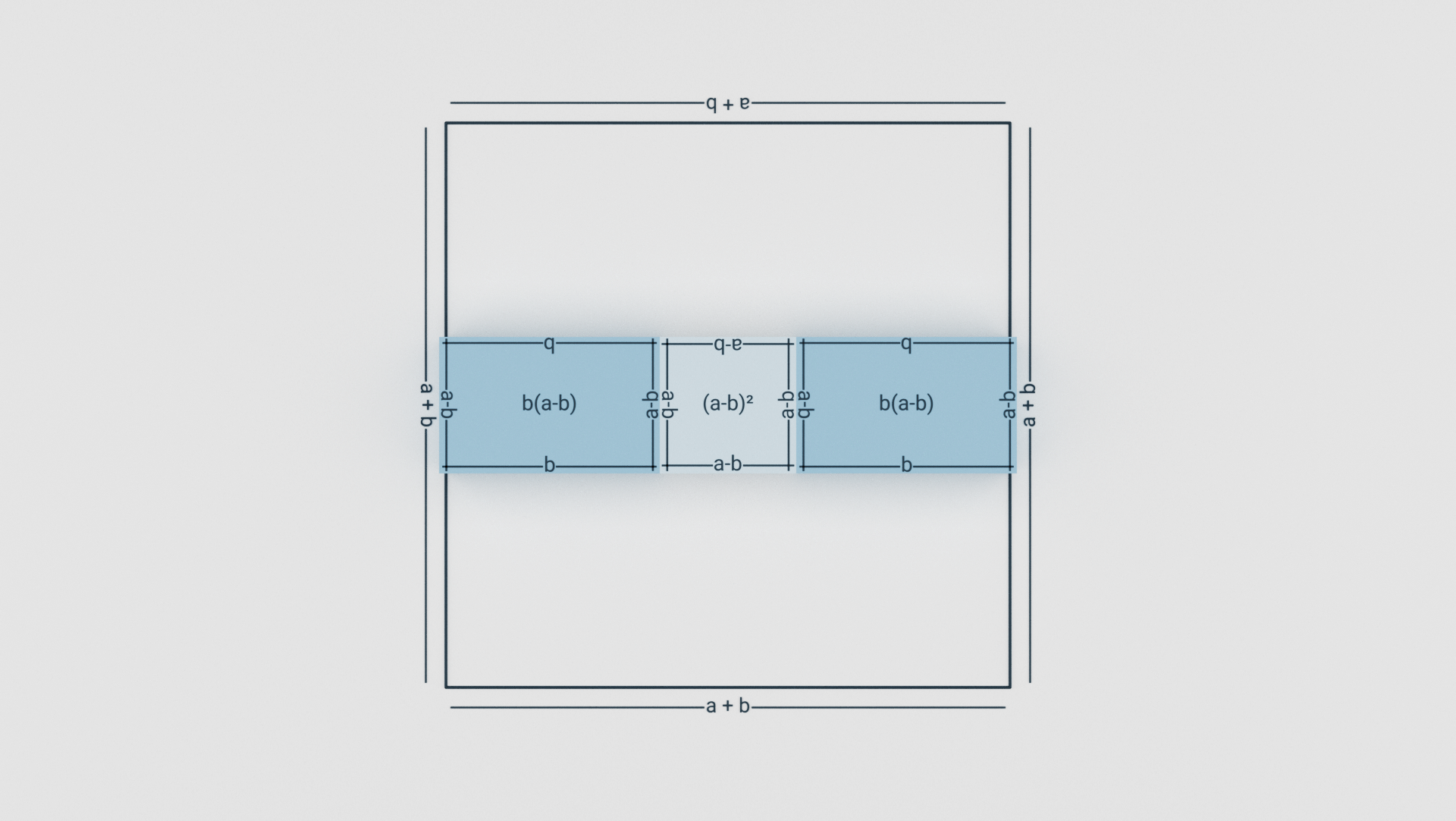
Now, length of this rectangle is b + (a – b) + b which is (a + b).

Breadth of this rectangle is (a – b).

As we all knew that Area of rectangle = length.breadth . So, Area after rearranging is (a + b).(a – b)

And before rearranging Area = a² – b² .

So, a² – b² = (a + b)(a – b)