The distributive property states that an expression which is given in form of x(y + z) can be solved as x(y + z) = xy + xz. This distributive law is also applicable to subtraction and is expressed as, y(x – z) = yx – yz.

Let’s see how we can prove this with the help of ZCube.

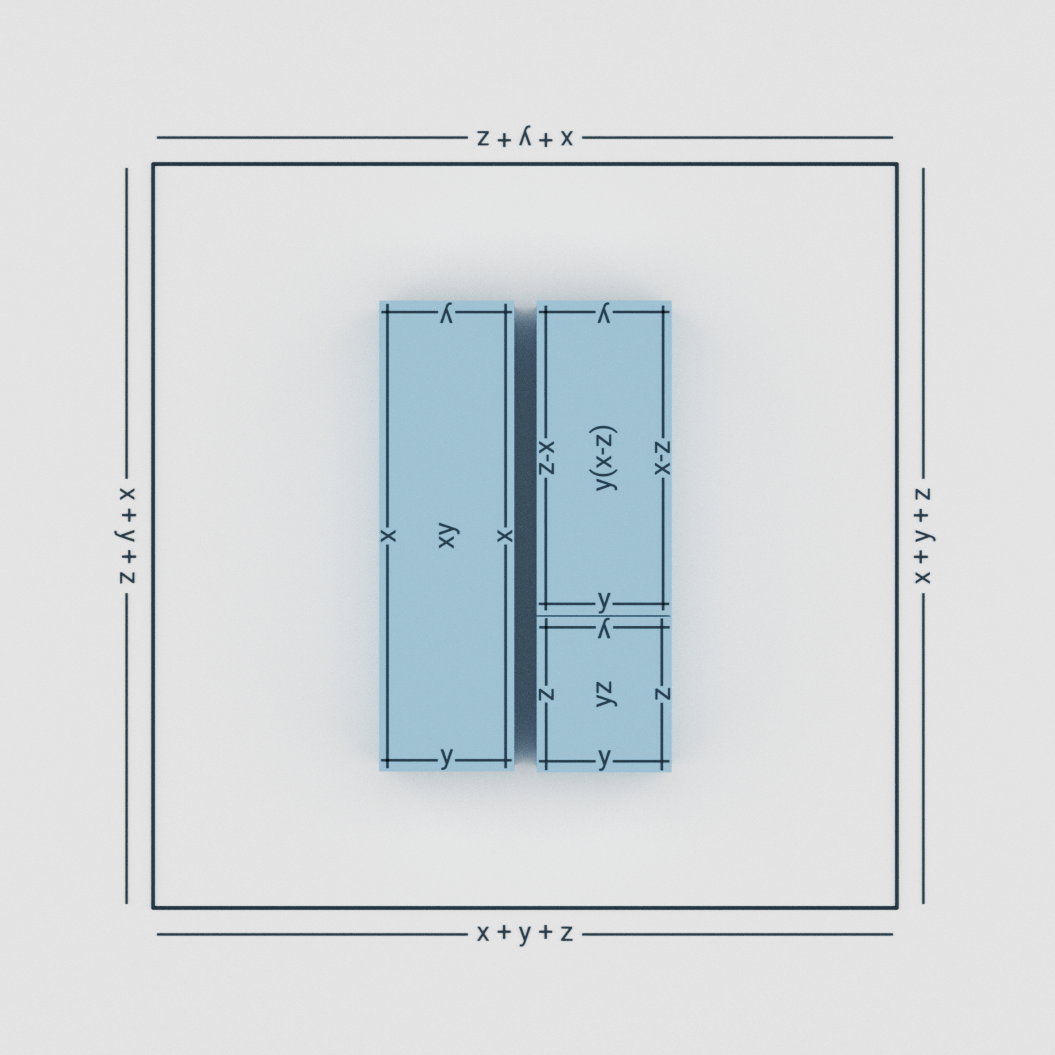
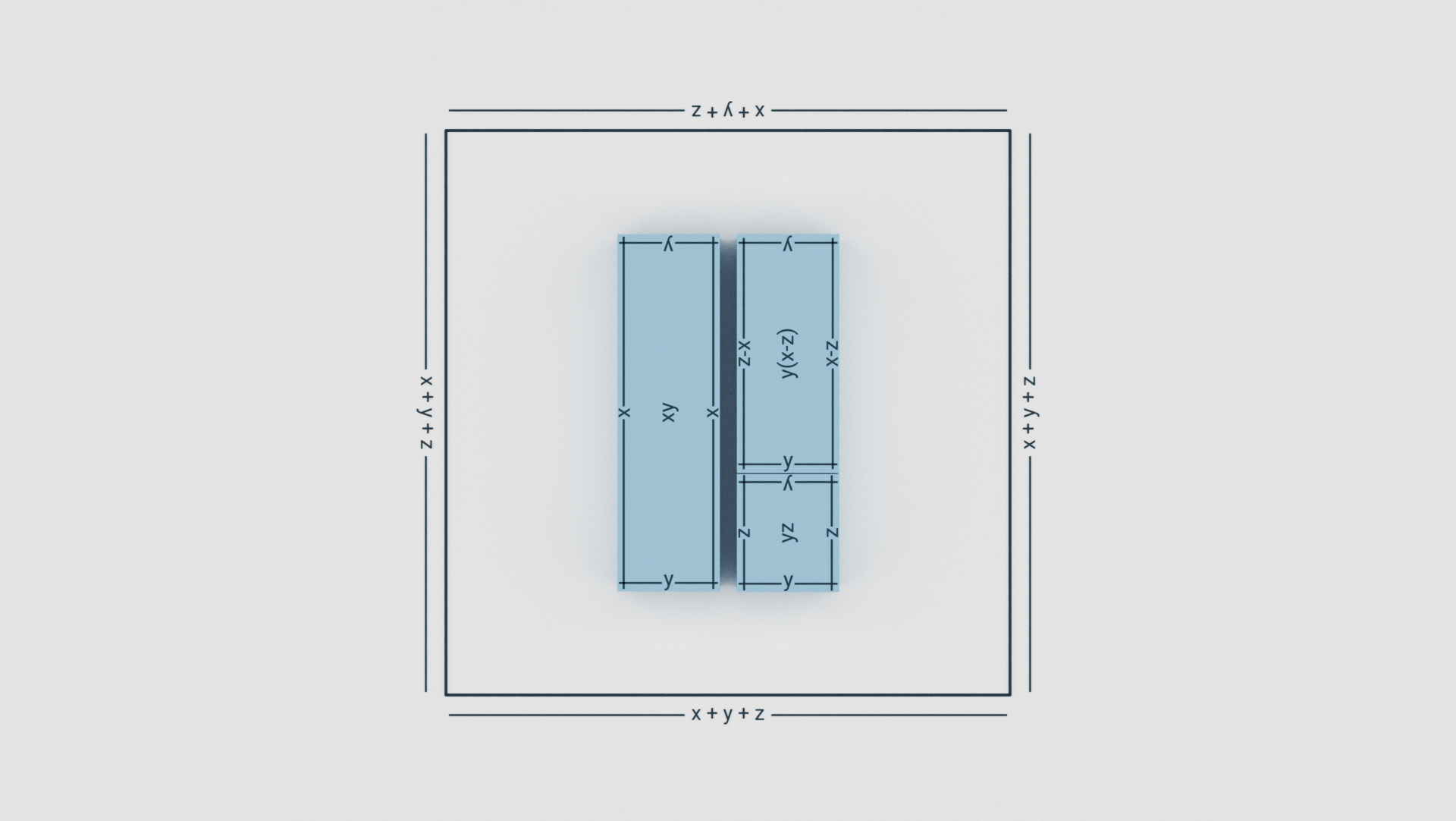
As you can see in the figure 3.1, we have xy, yz and y(x – z).

y(x – z) and yz are joined together to form a rectangle whose length is (x – z) + z which is x, and breadth is y. So, Area = xy.

Which means that y(x – z) + yz = xy.
So, y(x – z) = xy – yz.

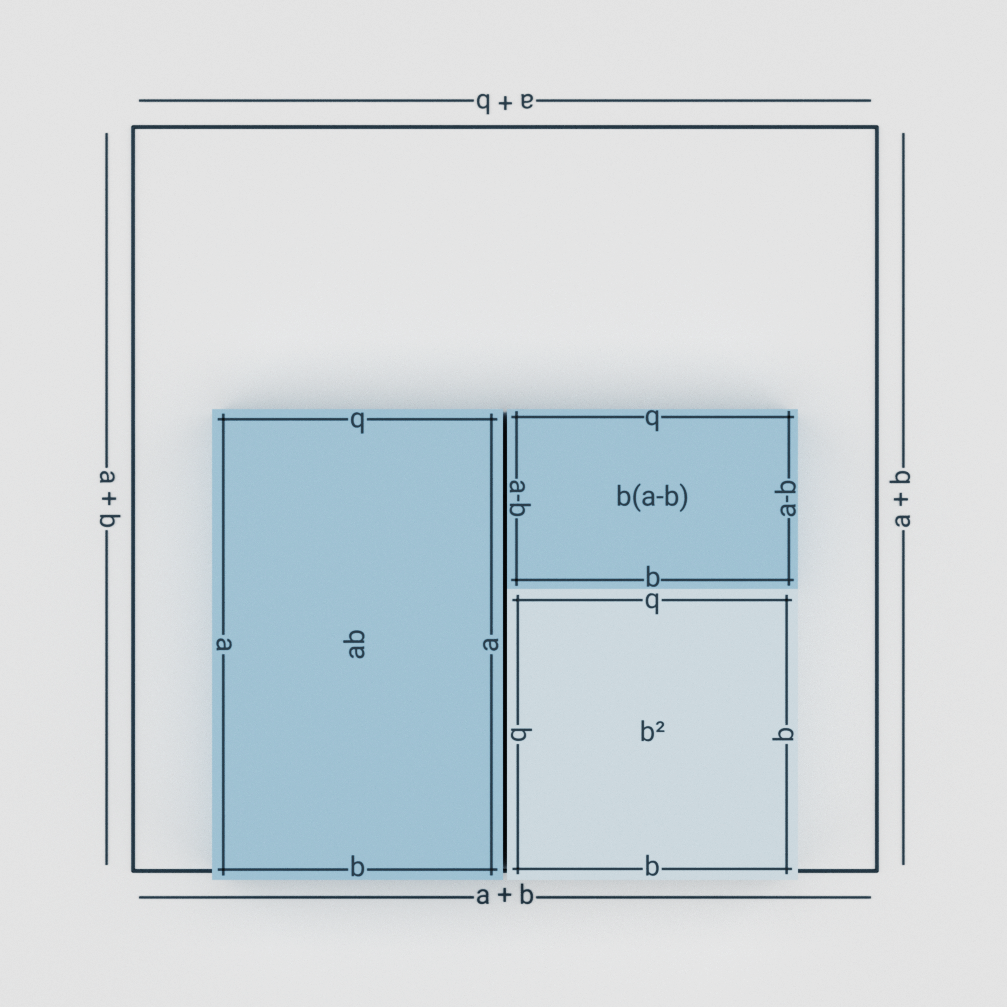
Similarly one can prove b(a – b) = ab – b².